Principiul cutiei - Dirichlet

Definiția cea mai simplă a principiului cutiei cunoscut și ca principiul lui Dirichlet se poate enunța astfel: Dacă se dă n+1 obiecte (de exemplu în matematică număr, punct, dreaptă, funcție etc.) dispuse în n cutii, atunci există cel puțin o cutie care conține două obiecte. Dacă în fiecare cutie ar fi cel mult un singur obiect, atunci în total am avea cel mult n obiecte.

Generalizare: Dacă plasăm kn+1 obiecte în n cutii, atunci cel puțin o cutie va conține cel puțin k+1 obiecte. De exemplu:

Exemplu 1. - Să se arate, că în fiecare comunitate se află 2 oameni, a căror cunoștințe printre cei prezenți sunt de același număr! (cunoștințele sunt reciproce)

Rezolvare: Presupunem că sunt n oameni în comunitatea respectivă. Atunci numărul cunoștințelor acestora pot lua următoarele n valori: 0, 1, 2, ..., n-2, n-1

Cum numerele 0 și n-1 nu pot apărea simultan, dintre n-1 numere diferite trebuie să alegem n numere, prin urmare avem între ele 2 identice.

 

Exemplu 2. - Să se demonstreze că printre orice 8 numere întregi există două a căror diferență este divizibilă cu 7.

Rezolvare: Să luăm prima dată un exemplu, fie cele 8 numere următoarele: 10, 15, 19, 20, 22, 25, 30, 35

După niște calcule, observăm, că 22-15=7 (divizibil cu 7).

Dacă ne gândim mai temeinic : scriind resturile obținute prin împărțirea numerelor date cu 7, aceste numere în ordinea dată sunt: 3, 1, 5, 6, 1, 4, 2, 0

Deoarece restul 1 apare de 2 ori : la împărțirea numerelor 15 respectiv 22, astfel diferența 22-15 ne dă restul 0, deci este divizibil cu 7.

Ne imaginăm, că avem 7 cutii ,cu inscripțiile următoare: 0, 1, 2, 3, 4, 5, 6.

Aceste ”inscripții” arată resturile obținute prin împărțirea numerelor respective cu 7. Pe figura alăturată se vede care dintre numerele enumerate trebuie puse în cutia respectivă.

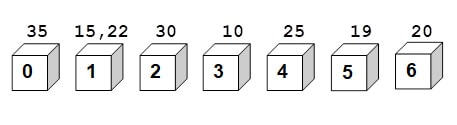
În general dacă se dă 8 numere, atunci în funcție de restul obținut prin împărțirea cu 7 se pot pune în cutiile de mai sus. Astfel va fi cu siguranță 1 cutie în care se află cel puțin 2 numere, iar diferența acestora va fi divizibilă cu 7.

Observație: Generalizând acest exemplu obținem următoarea proprietate (care se folosește deseori la problemele referitoare la teoria numerelor):

Între n+1 numere naturale există întotdeauna două care împărțind cu n dau același rest.

 

Principiul cutiei în Algebră

Dacă definim mai generalizat principiul cutiei, atunci acest principiu sună astfel:

Dacă n obiecte sunt puse în r cutii, unde r < n, atunci există cel puțin o cutie, care conține mai mult decât un obiect.

Această definiție în cazul funcțiilor ar fi: Dacă A și B sunt două mulțimi finite astfel că |A| = n > r = |B|

și f:A→B funcția asociată, atunci există b∈B astfel încât:

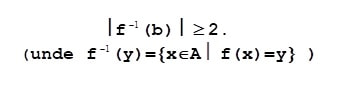
Mai mult, este adevărată următoarea Teoremă (cu notațiile de mai sus):

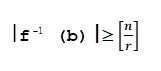inegalitatea (1)

Demonstrație: Dacă inegalitatea nu ar fi adevărată, atunci

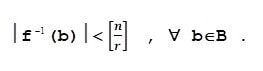
Dar cum mulțimea B are r elemente

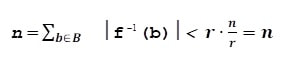
Ceea ce este imposibil, prin urmare există b∈B , pentru care inegalitatea (1) este adevărată.

 

Principiul cutiei în geometrie

Se dă un obiect geometric de ”măsura” T, în care așezăm forme diferite, forme care au ”suma măsurilor” mai mare, decât T. În acest caz există cel puțin un punct care este acoperit de 2-ori.

Generalizare: Dacă formele mai mici au ”suma măsurilor” mai mare decât k-T, atunci există un punct care este acoperit de k-ori.

Observație: În definițiile de mai sus noțiunile de măsură, obiect geometric și forme pot fi diferite. De exemplu obiectul geometric poate fi un interval, formele pot fi subintervale, iar măsura fiind lungimea intervalului; sau obiectul geometric poate fi un pătrat, formele pot fi cercuri, iar măsura poate fi aria.

 

Probleme de geometrie unde vom aplica Principiul cutiei

Problema 1: Colorăm punctele unui plan în alb sau negru. Să arătăm că există 2 puncte de aceeași culoare a căror distanță este egal cu 1 unitate.

Rezolvare: Considerăm un triunghi echilateral având latura 1 unitate. Dintre cele 3 vârfuri ale acestui triunghi există două care au aceeași culoare, iar distanța celor două puncte este exact 1 unitate.

 

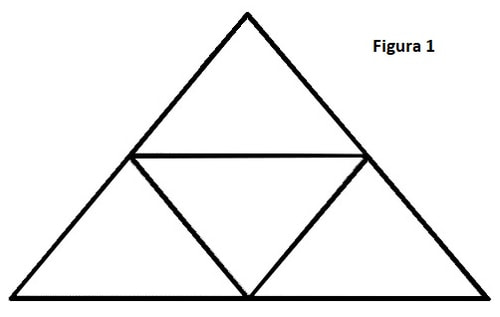
Problema 2: În interiorul unui triunghi echilateral cu lungimea laturii 2dm sunt plasate 5 puncte. Să se demonstreze, că există 2 puncte din cele 5 cu distanța dintre ele mai mică decât 1dm.

Rezolvare: Să divizăm triunghiul în 4 triunghiuri echilaterale congruente (fig.1) Deoarece sunt 5 puncte diferite pe 4 regiuni (triunghiuri) astfel obținute, există un triunghi în care se află 2 puncte din cele 5. Evident, distanța dintre cele 2 puncte este mai mică decât 1dm.

 

Problema 3: Se dă 5 puncte în sistemul de coordonate dreptunghic xOy a căror coordonate sunt numere întregi. Să se arate că dintre punctele date există 2 cu proprietatea că mijlocul segmentului determinat de ele are coordonatele numere întregi.

Rezolvare: Coordonatele mijlocului unui segment se calculează făcând media aritmetică a absciselor, respectiv a ordonatelor capetelor segmentului. Prin urmare aceste numere vor fi întregi daca coordonatele corespunzătoare ale capetelor segmentului au aceeași paritate, deci suma lor este număr par.

Cum avem 5 puncte date, dintre ele există cel puțin 2 care au proprietatea cerută, fiindcă ceea ce privește paritatea avem 4 posibilități de a determina cele 2 coordonate: par - par, par - impar, impar - par, impar - impar .

 

Bibliografie:
Kása Zoltán-Bege Antal: Matematică discretă Univ. Babeș-Bolyai, Cluj-Napoca, 2002;
Mitrinovic, D.S.-Sándor, J.-Cristici, B. : Handbook of Number theory. Kluwer Academic Publisher,Dordrecht,1996;
Sárközy András-Surányi János: Számelmélet-feladatgyűjtemény. Tankönyvkiadó, Budapest,1986.