Transformări care păstrează aria

În această lucrare mi-am propus să prezint câteva procedee de transformare a unui triunghi într-un triunghi echivalent cu el, a unui patrulater oarecare într-un triunghi echivalent cu el, a unui pentagon oarecare într-un triunghi echivalent cu el, a unui paralelogram dat într-un alt paralelogram a cărui bază să fie congruentă cu un segment dat, a unui dreptunghi într-un pătrat echivalent cu el, a unui triunghi într-un triunghi dreptunghic echivalent cu el care să aibă ca ipotenuză una din laturile triunghiului.

 

Problema 1. Să se demonstreze că, dacă baza unui triunghi este fixă și vârful opus se mișcă pe o paralelă la ea, aria triunghiului rămâne constantă.

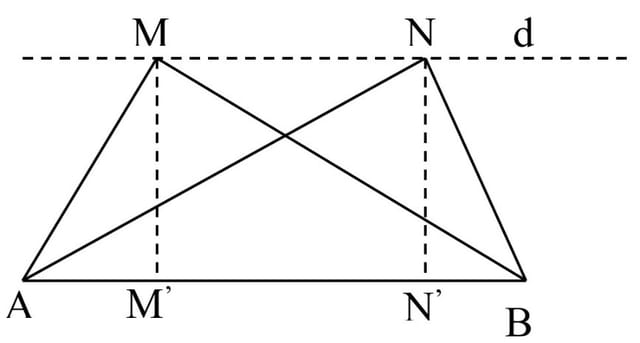
Rezolvare: Fie MAB un triunghi și d o paralelă la AB. Când vârful M se mută în N, se obține triunghiul NAB. Baza triunghiului s-a schimbat, dar nu și înălțimea.

Observație: Pe baza acestei propoziții un triunghi oarecare MAB se poate transforma într-un triunghi NAB echivalent cu el care să aibă aceeași bază AB. Vârful N poate fi orice punct al paralelei d, așa că i se poate impune o condiție suplimentară, ca în problemele următoare.

 

Problema 2. Să se transforme un patrulater dat într-un triunghi echivalent cu el, care să aibă o latură și un unghi alăturat comune cu el. În câte moduri se poate face transformarea? Să se examineze și cazul când patrulaterul dat nu este convex.

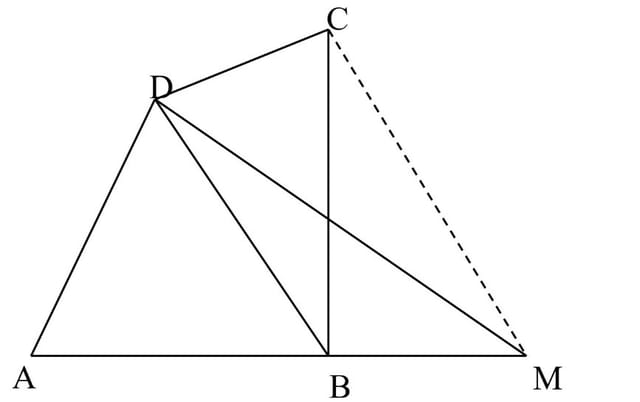
Rezolvare: Fie ABCD un patrulater dat. Se duce prin vârful C, de exemplu, paralela la diagonala BD. Fie M intersecția ei cu dreapta AB. Triunghiul AMD este cel căutat deoarece partea ABD este comună patrulaterului și triunghiului, iar triunghiul BDM este echivalent cu BDC.

Dacă se folosește diagonala BD, vârful C se poate muta pe dreapta AB sau AD, vârful A se poate muta pe dreapta BC sau CD, deci transformarea se poate face în patru moduri. Dacă se folosește diagonala AC, apar alte patru moduri. În total, construcția se poate face în opt moduri.

În cazul patrulaterului neconvex ABCD se face aceeași construcție. Triunghiul AMD este echivalent cu patrulaterul ABCD. Într-adevăr, prin trecerea de la patrulater la triunghi, se scade triunghiul NMB și se adaugă NCD. Dar, triunghiurile BDC și BDM sunt echivalente, partea BDN le este comună, deci triunghiurile NMB și NCD sunt echivalente.

 

Problema 3. Să se transforme un pentagon dat într-un triunghi echivalent cu el.

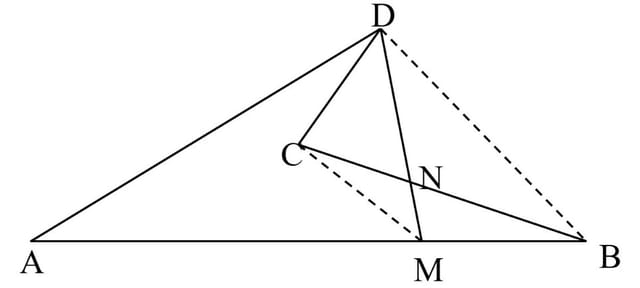
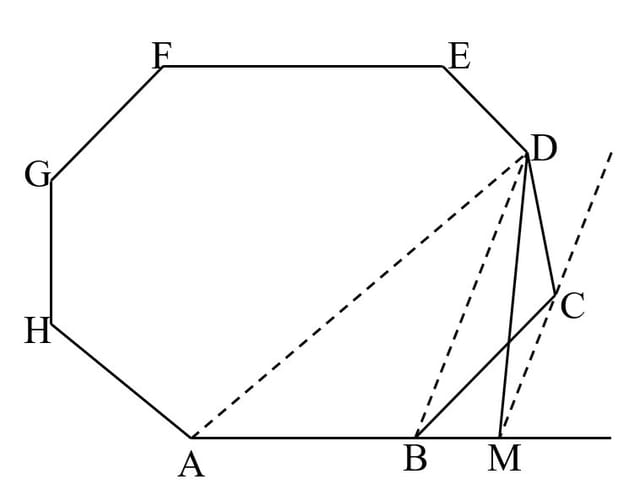
Rezolvare: Fie ABCDE pentagonul dat. Se duce diagonala CE și după procedeul anterior, patrulaterul ABCE se transformă în triunghiul MCE echivalent cu el. Pentagonul inițial devine patrulaterul MCDE echivalent cu el. Paralela prin D la CE intersectează ME în N. Triunghiul MCN este cel căutat.

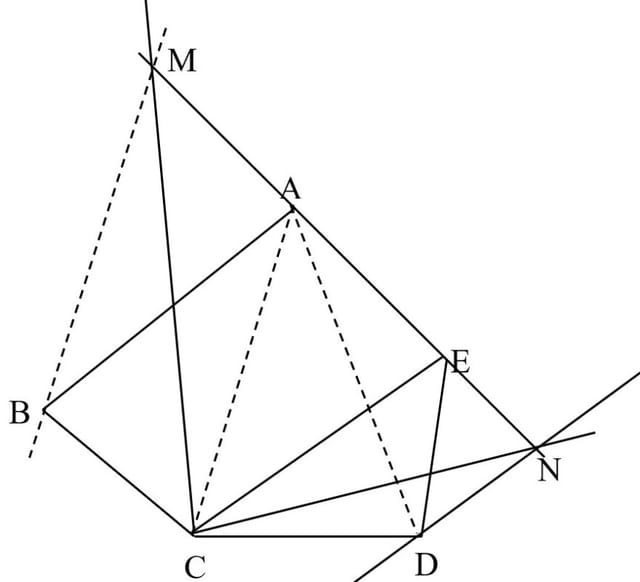
Observație: Prin acest procedeu se poate transforma orice poligon într-un triunghi.

Într-adevăr, în cazul unui poligon ABCDE… se duce diagonala AD și, după procedeul de mai sus, patrulaterul ABCD se transformă în triunghiul AMD echivalent cu el. Poligonul inițial devine AMDEF… echivalent cu el și are o latură mai puțin (vârfurile B și C au dispărut și în locul lor a apărut un singur vârf, M). Procedeul se repetă până când se obține un triunghi.

 

Problema 4.
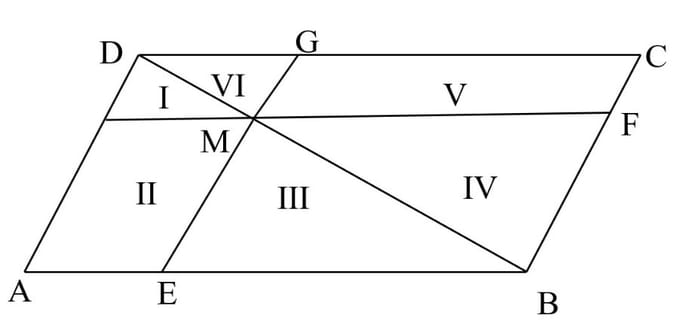
a) Fie ABCD un paralelogram. Printr-un punct M al diagonalei BD se duc paralelele la laturile sale și se notează cu E, F, G și H intersecțiile lor cu laturile paralelogramului E∈AB, F∈BC, G∈CD.
Să se demonstreze că paralelogramele AEMH și MFCG, pe care nu le traversează diagonala, sunt echivalente.

b) Aplicație: Să se transforme un paralelogram dat într-un alt paralelogram a cărui bază să fie congruentă cu un segment dat.

Rezolvare:

a) - O diagonală a unui paralelogram împarte paralelogramul în două triunghiuri congruente. Notăm ariile părților așa cum se vede în figură. Atunci: I+II+III=IV+V+VI.

Dar I=VI și III=IV, deci II+V.

b) - Fie AEMH paralelogramul dat și a segmentul dat. Se prelungește AE cu un segment EB congruent cu a; fie BM∩AH={D}. Prin B se duce paralela la AD și prin D paralela la AB; fie C intersecția lor. Se prelungește EM și HM până la intersecția lor cu DC și BC în G și F. Paralelogramul MFCG este cel căutat.

Observație: Propoziția de mai sus este valabilă și în cazul particular când patrulaterul ABCD este dreptunghi, construcția indicată arată cum se poate transforma un dreptunghi într-un dreptunghi echivalent cu el care să aibă o latură dată.

În antichitate, această transformare era foarte importantă. Matematicienii greci nu făceau, ca noi, operații cu lungimile segmentelor, care sunt numere, ci cu segmentele însăși. Pentru ei, produsul a două segmente a și b era un dreptunghi cu laturile egale cu a și b. Atunci o expresie ca ab+cd, în care a, b, c, și d sunt segmente, era o sumă de două dreptunghiuri. Ca această sumă să fie tot un dreptunghi, unul din cele două dreptunghiuri trebuie transformat astfel încât una dintre laturile lui să fie congruentă cu o latură a celuilalt. Construcția se făcea prin procedeul descris mai sus. Dreptunghiul astfel transformat se putea “lipi" de celălalt.

 

Problema 5. Să se transforme un dreptunghi într-un pătrat echivalent cu el.

Rezolvare: Fie a și b dimensiunile dreptunghiului și x latura pătratului. Condiția este x2=ab. Se construiește media proporțională x a segmentelor a și b.

 

Problema 6. Să se transforme un triunghi într-un triunghi dreptunghic echivalent cu el care să aibă ca ipotenuză una dintre laturile triunghiului. În ce caz are problema o soluție?

Rezolvare:

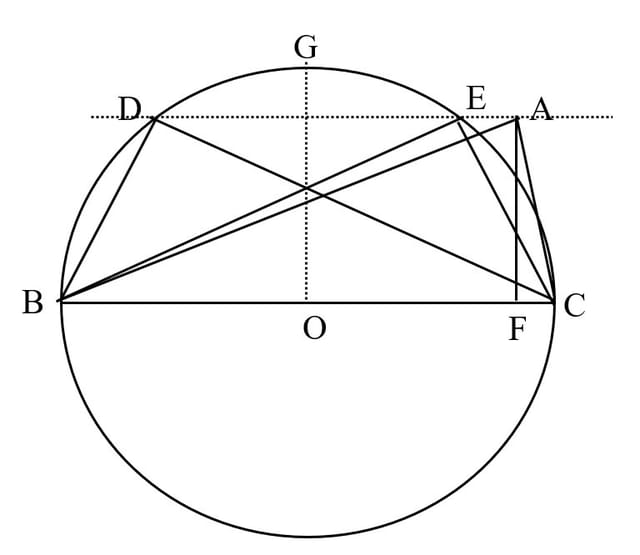
Fie ABC triunghiul dat. Prin A se duce paralela la BC și se construiește un semicerc cu diametrul BC; fie D și E punctele lor de intersecție. Triunghiul căutat este DBC sau EBC. Sunt în aparență două soluții, de fapt aceste triunghiuri sunt congruente. Condiția ca problema să aibă o soluție este ca paralela la BC dusă prin punctul A să taie cercul. Fie AF înălțimea triunghiului și OG raza perpendiculară pe BC. Condiția ca paralela să taie cercul este AF ≤ OG. Dar OG =, deci condiția ca problema să aibă soluție este AF ≤ , adică înălțimea triunghiului să fie cel mult egală cu jumătate din bază. O latură a triunghiului ABC poate fi luată ca ipotenuză numai dacă înălțimea corespunzătoare este mai mică decât jumătatea ei.

 

Bibliografie:
A.Hollinger, Probleme de geometrie, Editura didactică și pedagogică București, 1982